Defying Gravity: Must What Go Up, Always Come Down?

What goes up must sometimes come down… but not always. An object traveling at escape velocity will no longer fall back to Earth due to gravity’s pull.

The tension in the playground was palpable. The players of the two teams stood facing each other, hand in hand forming chains that would not be breached. A name was called out and the chosen player from Team A emerged. Team B braced itself for attack. If this player was able to break through their chain of linked arms, Team A would win.

Brows furrowed in concentration and face ablaze with determination, the player made a dash for it…

Achieving escape velocity was perhaps just as challenging on the playground as it is during space travel!

The common understanding associated with gravity is limited to its relation to the ground beneath our feet. Gravity wants to draw us toward the Earth (a force we experience as our weight) and the Earth to us; however, Earth’s massive size makes its movement towards us imperceptible, i.e., even though we pull the Earth a little bit towards us, it goes unnoticed because of the Earth’s much greater mass. The greater the mass of an object, the harder it is to move it – a phenomenon expounded in Newton’s first law of motion.

A math book (no matter how gleefully) tossed into the air from Earth falls back down, as it does not have sufficient energy to break free from Earth’s gravitational pull. Throw the book higher and it will spend more time in the air before eventually coming back to Earth, but return it will. What goes up, must come down, right? However, if that were always the case, how do satellites and rockets stay up without falling back to Earth?

How To Get Away From Gravity

As part of a thought experiment, let’s imagine Newton, sitting peacefully under a tree trying to decipher the mysteries of the universe, when he is suddenly struck on the head by an apple. In a fit of genius, Newton tosses the apple that had landed on his head heavenwards, slightly peeved, as one would be after being bonked on the head by an unwanted fruit. However, Newton has an epiphany! The apple he just flung into the air would travel indefinitely if it weren’t for gravity, which causes its descent, and atmospheric friction, which makes it decelerate.

Newton wondered if gravity, which made the apple fall, could extend in reach beyond the Earth and its constituents – to the moon and other planets. He proposed that objects falling to the ground and the movement of planets around the sun could both be explained by the same principle.

Newton realized that it would be possible to send an object from Earth into space if the object were to be projected from the surface of the Earth with sufficient velocity. Known as escape velocity, this is the minimum velocity that will allow a body to release itself from the grips of the gravitational pull of another body and travel to infinity without falling back. So… how hard must one toss something skywards so that it does not come back?

Imagine being trapped at the bottom of a well. In order to escape, one would need to expend energy to climb out. The escape velocity is a measure of the precise amount of energy required to arrive at the mouth of the well.

Also referred to as the ‘second cosmic velocity’, the escape velocity from Earth happens to be about 11.2 km/s. For a given velocity, a spacecraft designed to travel into space will be able to achieve orbit around Earth or other celestial objects. To break free of such an orbit, a greater velocity is needed. The term ‘Cosmic velocities’ was coined by Russian scientists to describe the important velocities associated with space travel.

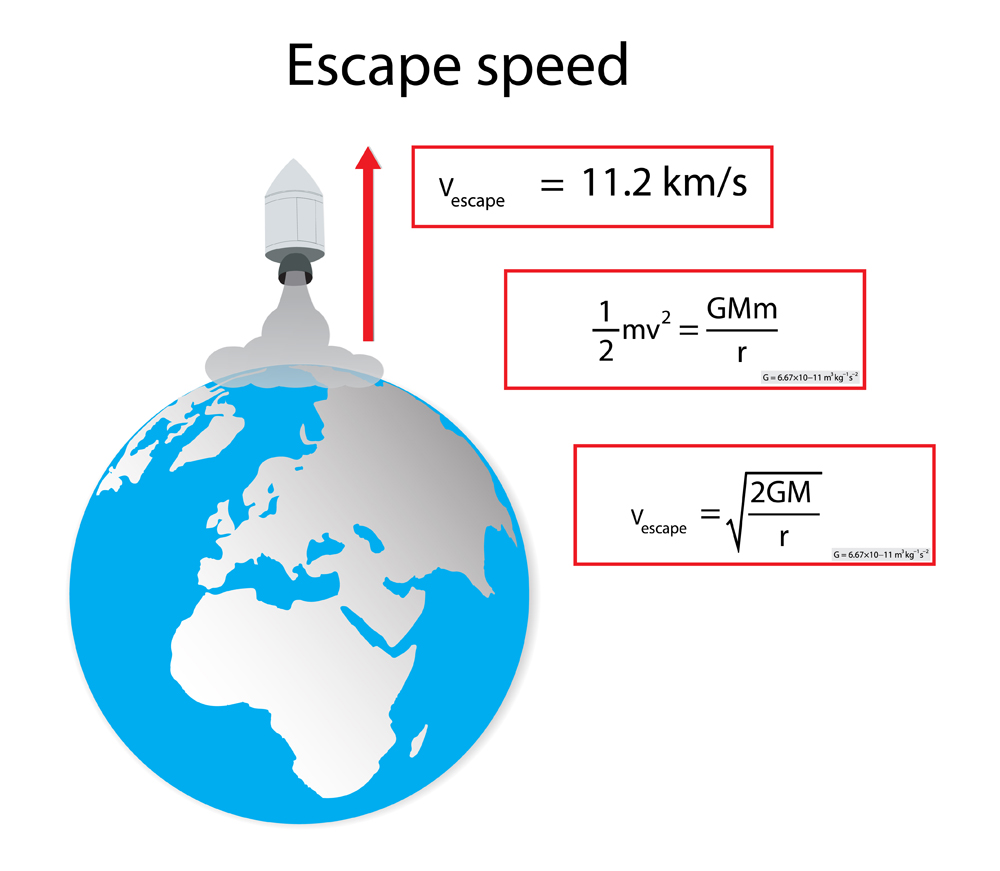
The ‘first cosmic velocity’, known as the orbital velocity, causes a projectile to revolve around the cosmic body. A slower projectile that is traveling at a speed less than the orbital velocity will fall back to Earth, albeit gradually. A spacecraft, however, need not reach escape velocity to travel to space.

The International Space Station (ISS) orbiting the Earth cruises at a speed of approximately 7.9 km/s. With its engines turned off, it is in a state of perpetual free fall, but it goes around the Earth with a speed that is just great enough to keep it from falling.

This is somewhat analogous to the spinning action of a yo-yo. Any spinning object has an angular momentum associated with it, but the string around the yo-yo’s axle is pulling it in at all times so that it does not travel off in a straight line due to the momentum provided. Similar to this, the Earth’s gravity keeps the ISS in its orbit so that it continues its revolution around the Earth.

Einstein, in his theory of general relativity, posited that gravity is not a force between masses, but rather a distortion in the fabric of space-time caused by the presence of mass. Similar to how a line drawn on a sheet of paper will not appear to be straight if the paper is twisted, the straight path of an object will also be bent when space-time is warped. Since gravity warps spacetime in a manner such that the straight paths of all objects are curved in the same way near the Earth, all objects fall at the same rate.

This has important implications in terms of escape velocity. If the escape velocity associated with a gravitational field approaches the speed of light, the gravitational field is considered strong. A smaller escape velocity indicates a weak field. For low speeds and weak gravitational fields, the results obtained from the general theory and Newton’s theory are approximately the same.

Also Read: What Is Escape Velocity?

Escaping From A Black Hole?

Escape velocity depends on two parameters—the mass of the object whose gravitational pull has to be superseded and the distance to the center of mass of that object. To break free from Earth’s gravity, a rocket must accelerate to 11.2 km/s, but for escaping from a planet with the same mass as Earth, but half its diameter, the escape velocity would have to be different. Since the diameter is halved, the distance from the planet’s surface to its center of mass reduces, and the escape velocity increases.

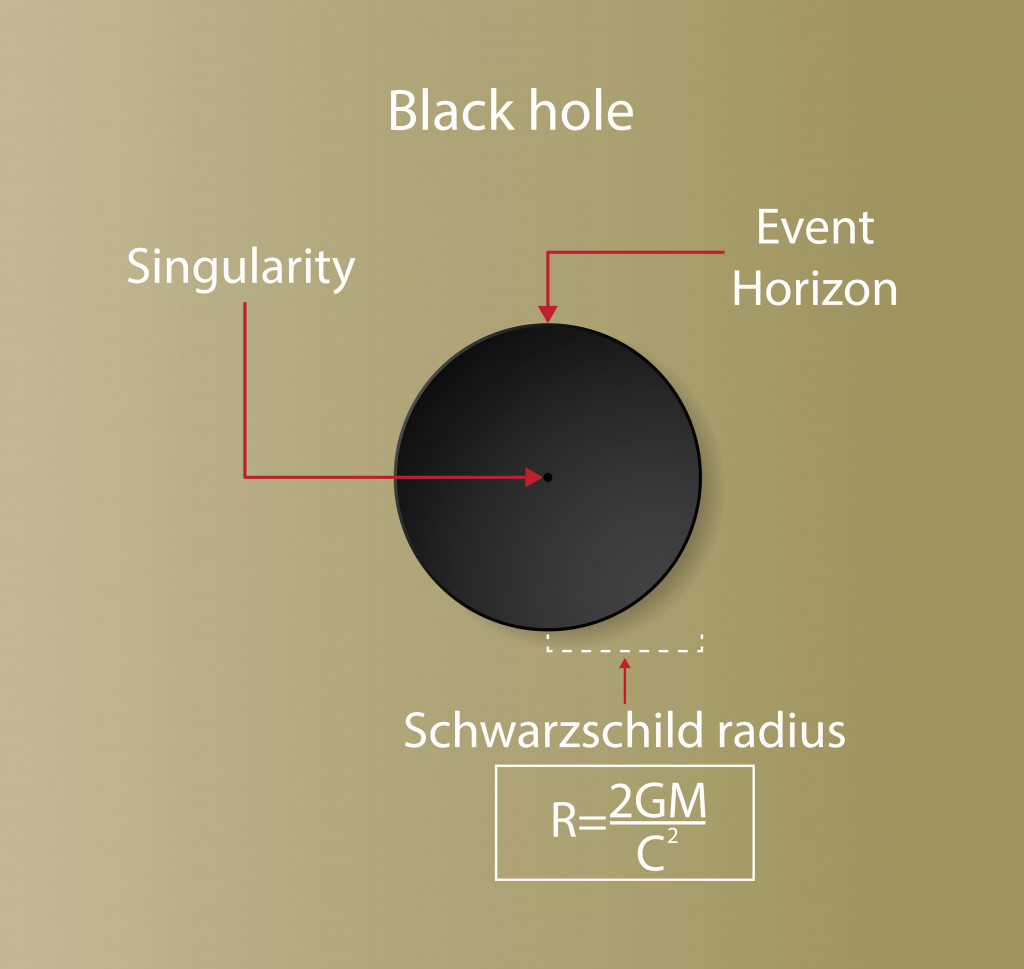
At a critical radius known as the Schwarzschild radius, a gravitational mass has an escape velocity equal to the speed of light. In the 18^th century, using Newton’s law of gravitation, John Michell proposed that light leaving the surface of a sufficiently massive star could not escape.

Michell’s calculations did not give correct estimations, but almost a century later, Karl Schwarzschild showed that when a body collapses beyond the Schwarzschild radius, it is fated to become a black hole, since the Schwarzschild radius is the limit at which gravity triumphs over all other forces. Thus, to escape the intense gravitational pull of a black hole, an escape velocity greater than the speed of light is needed.

Also Read: How Close Must You Come To Earth To Be Influenced By Its Gravity?

We All Need To Be Lifted At Times

One might ask, does the concept of escape velocity apply to birds and airplanes too? What about helium balloons?

Here’s the answer: escape velocity is required only when an object is trying to break free from another body’s gravitational tug. To put it simply, an airplane doesn’t have to attain escape velocity for flying, because it is not trying to escape from Earth. Neither does it need to be in orbit around Earth.

However, this means that in order to keep flying, it must constantly overcome the downward acceleration due to gravity, which it does by generating lift using its wings and engines.

Birds also sustain flight utilizing the same principle, with their wings producing low and high pressure above and under the wings, such that lift can be achieved. The key component here is the presence of air, without which it would not be possible be to create change in air pressure and, in turn, lift.

Helium balloons are filled with helium, which is lighter than air. When a heavy gas (more dense) interacts with a light gas (less dense), the lighter one floats on top. A helium balloon rises in the air until it attains an atmospheric height at which the density of the air inside the balloon is equal to the density of air outside it. This generates the required lift.

In theory, at least, an object may travel at velocities other than the escape velocity and still be able to completely lift itself out of a planet’s gravitational field. The escape velocity has been defined for non-propelled objects only, i.e, an object traveling at escape velocity will need no further impetus to escape.

To exit Earth at a velocity less than the escape velocity, one would need to provide a continuous boost to the object to overcome gravity for the entire duration of the flight. For a spacecraft, this means external support in terms of several booster rockets to maintain a continuous thrust to counter Earth’s gravity – a thrust that is generated by the burning of an indescribably vast amount of fuel. Not only would this be a huge waste of propellants, but trying to escape Earth or even reach orbit in this manner, while carrying such enormous amounts of fuel, would be highly impractical.

Gravity remains ubiquitously influential, even as its pull weakens with increasing distance. Traveling higher only reduces its sphere of influence, but one may never truly escape it. However, with a bit of luck and the right velocity, it might be possible to evade its siren call!

How well do you understand the article above!

Can you answer a few questions based on the article you just read?

Start Quiz

Question

Your answer:

Correct answer:

Next

You got {{SCORE_CORRECT}} out of {{SCORE_TOTAL}}

SHARE YOUR RESULTS

ShareTweetPinEmail

Your Answers

Retake Quiz