Table of Contents (click to expand)
No, a straight line isn’t always the shortest distance between two points. The shortest distance between two points depends on the geometry of the object/surface in question. For flat surfaces, a line is indeed the shortest distance, but for spherical surfaces, like Earth, great-circle distances actually represent the true shortest distance.
All of us were taught at an early age that ‘a line is the shortest distance between two points’. However, what if someone told you this time-honored adage wasn’t exactly true—would your reality be able to handle it?
As it turns out, the statement is only partly true. The shortest distance between two points actually depends on the geometry of the object in question.
If we were living on a flat earth (which we don’t) then yes, a straight line would be the shortest distance between points A and B. However, the Earth is an approximate sphere, and the shortest distance between two points on the surface of a sphere is an arc known as ‘the great circle distance’.

Great Circle Distance
Great circle distance isn’t a new concept; in fact, many of you have already seen it in action.
People who have traveled by air or solely checked flight routes have probably noticed that flights don’t follow a direct path, but instead take a curved route to their destination. The curved routes aren’t employed to dig a deeper hole in the passenger’s pockets, but are used because they’re actually the shortest distance between any two given locations on our planet.
These curved routes are often confusing, as the routes are outlined on a flat 2-dimensional map, where a straight line might seem like the shortest distance. However, no 2-dimensional map of the Earth is accurate. Not even the one we grew up learning, which is the same as you would find in Google maps.
To give you the gist, our beloved Earth is a 3-dimensional space and is best represented using a model globe. However, when one tries to flatten the sphere into a rectangular shape, as most maps do, the age-old dilemma of distortion comes into the spotlight. Most rectangular maps trade country shapes, sizes, intermediate distance, and even legitimate information for ease of understanding. For more details on this matter, read What’s wrong with all our maps?

Imagine that you want to fly from the rat-infested depths of New York City to the City of Love, Paris. On a globe, the shortest distance between the two cities would be an arc of roughly 3,630 miles, but the same arc, when projected on a 2D map, transforms into a straight line measuring approximately 3,750 miles.
To confirm this for yourself, open Google Maps in an adjacent tab and search for New York. Once found, right-click on the name tag and select “measure distance”. Next, zoom out or scroll a bit to the right to find Paris and click on it. The following distance will be a curve, representing the shortest distance between the two cities. Click anywhere on this curve to make a keyframe and drag it a little towards the south to convert the curve into a straight line. You can make use of multiple keyframes to compose a straight line of some sort between the two locations. Upon completion, compare the dimensions of the curve and the straight line (and prepare for your reality to be shattered!).
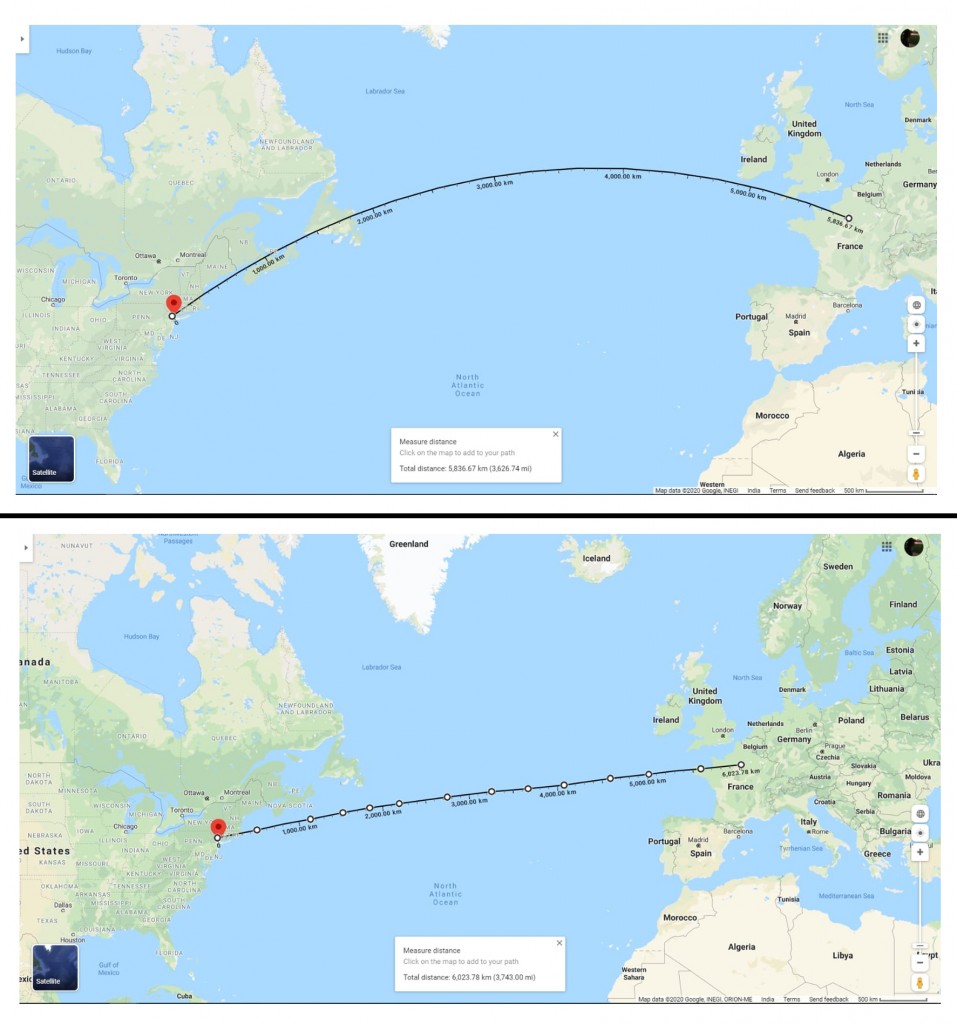
The difference between the two numbers (3,750 – 3,630 = 120 miles) may not seem like a big deal, but considering the fact that a Boeing 747 consumes an average of 5 gallons of fuel per mile of flight (Source), the plane would require an additional (5 gallons/mile × 120 miles =) 600 gallons (2250 liters) to traverse the extra distance, which is a big deal and would add to the cost of plane tickets.
Also Read: What’s Wrong With All Our Maps?
Great Circle Distance In Mathematical Terms
Speaking in purely mathematical terms, a great circle (also known as geodesics of spheres) is any circle drawn on a sphere whose center coincides with the center of the sphere, and thus divides the sphere into two equal halves. In simpler terms, a great circle is the largest circle that can be carved out of a sphere. A small circle, on the other hand, is when the center of the circle and the sphere do not coincide.
Imagine (or just check the below image) cutting the Earth along the equator or the poles. The resulting hemispheres in both cases would be equal, and the faces of these hemispheres would have the same diameter and center as the sphere (Earth) itself.
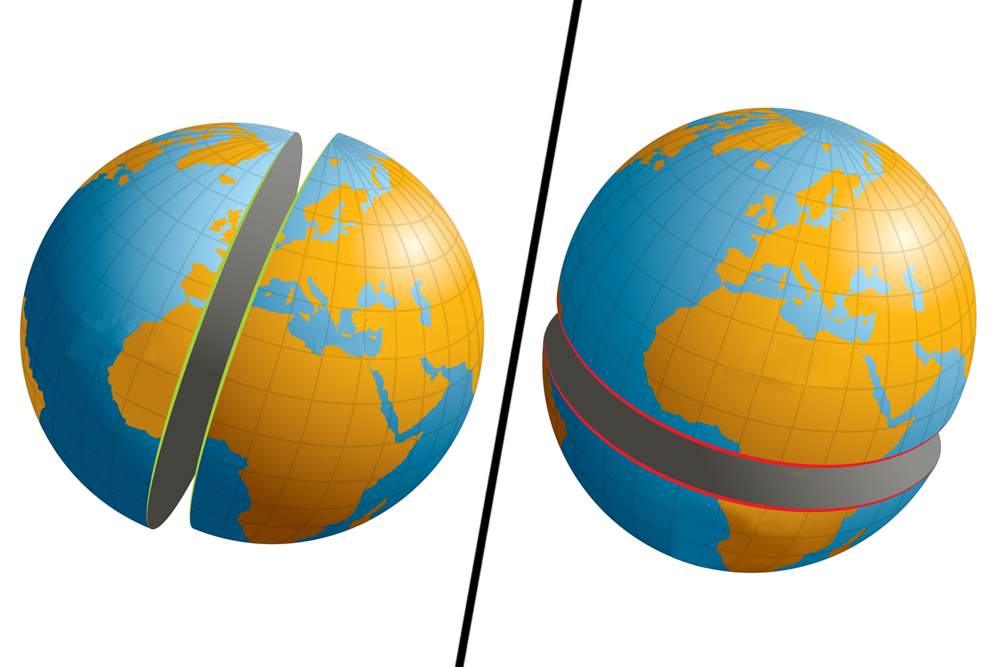
For any two non-diametrical points (locations) on a sphere (Earth), there exists only one unique great circle, whereas for diametrical points on a sphere, an infinite number of great circles can be drawn. These points divide the circle into two arcs; the smaller arc represents the true shortest distance between the two points and is called the great-circle distance.
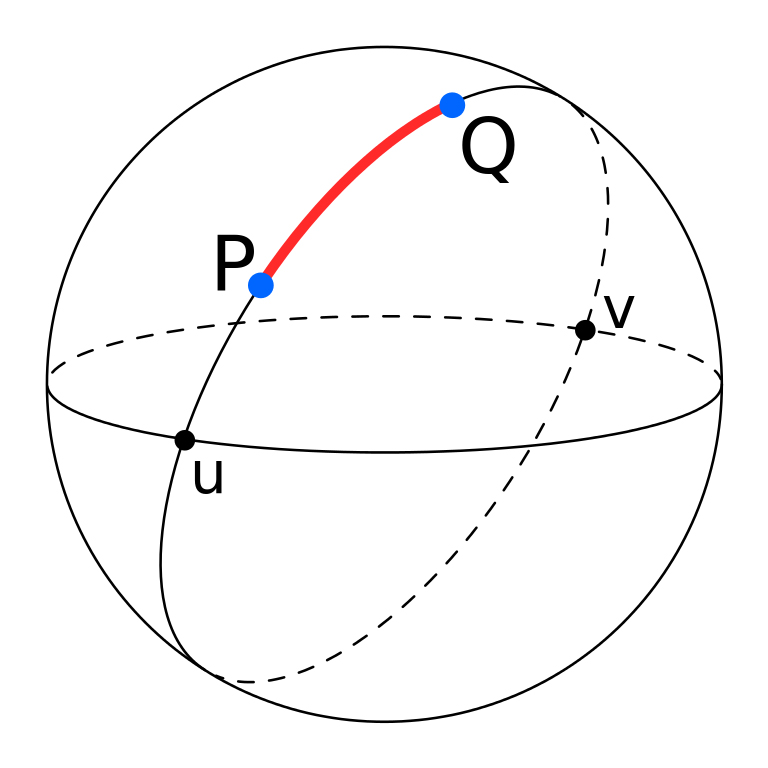
In the below image, the points P and Q are two non-diametrical points and the arc PQ represents the shortest distance between the two (great circle distance). The points u and v, on the other hand, are known as antipodal or diametrically opposite points, and divide the great circle into two identical arcs.
Calculating great circle distance between any two points on the surface of a sphere requires the use of spherical trigonometry, and while we might not have been familiar with the existence of great circle distances back in our school days, everyone’s hatred for sines and cosines is a well-known fact.
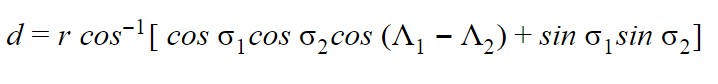
Here, d is the great circle distance, r is the radius of the sphere (Earth) and the term cos-1(cos σ1 .cos σ2 .cos (λ1 – λ2) + sin σ1 .sin σ2) is the central angle subtended by the two points having coordinates σ1, λ1 and σ2, λ2 respectively.
Also Read: How To Find The Radius Of The Circle?
Final Words
As stated earlier, great circles find their main application in long-distance travel, particularly air and naval navigation. The curved nature of great circle distances, supplemented by the rotation of our planet, has pilots and sailors constantly adjusting their course. A great circle distance is therefore broken down into ‘Rhumb lines’, which represent a constant direction.
Having said all that, even great circle distances do not represent the true shortest distance between two given locations. The great circle distances are calculated assuming Earth to be a perfect sphere, but the planet is more of a flattened sphere with different values of radius towards the equator and the poles. The great circle values thus have a tolerance of about ±5%.
Nevertheless, great circle distances have played a huge role in long-distance travel over the past several years and will continue to do so, saving airlines fuel and saving travelers money!
Also Read: Is Earth A Perfect Sphere?
How much do you know about straight lines and great distances?

