Table of Contents (click to expand)
A natural logarithm is a logarithmic function with base “e” that is found repeatedly in nature.
Math is something I prefer to think of as a language. More specifically, it is the language of the universe. Some numbers, like some words in every language, are always used, while others basically exist only in the dictionary. Other than ordinary numbers, math also has cool symbols to represent certain numbers. “π” (pi) is a popular one, along with “i” (iota)—the root of negative one, and many more.
Another well-known one is “e” (Euler’s number), the base of natural logarithms. The value of e goes like 2.7198281828459…
What makes an irrational and transcendental number like “e” special? Or what makes the natural log so “natural”?

What Is A Natural Logarithm?
Logarithms are reverse exponential operators. It is the value of power that a number should be raised to get another number.
For instance, log2 8 = 3, which implies 23 = 8. Here, subscript 2 is the base of the logarithm, and 2 raised to the power 3 will give 8. So, if we take the log of 8 with base 2, the answer will be 3.
Similarly, loge (x) is known as the natural logarithm of a number x, or simply denoted as ln(x). That is, eln(x) = x or ln ex = x.
Also Read: What Is I Raised To The Power I?
History Of Logarithms And Natural Logarithms
Despite the fact that logarithms are described as reverse exponential operators, which is correct in the modern sense, it is not why they were invented. When John Napier first published his discovery about logarithms in 1614, logarithms were used as calculation tables.

You can basically consider those log tables as a more advanced version of multiplication tables. Logarithms were used to simplify complicated multiplication and division calculations to addition and subtraction. Of course, this was back in the pre-computer, pre-calculator era, when even multiplications were time-consuming. Most of us don’t come across logarithmic tables these days.
What’s more surprising is that natural logarithms were discovered decades before e was discovered. It’s true, even though it doesn’t make much sense.
This table can be used to demonstrate a very simple logarithm table.
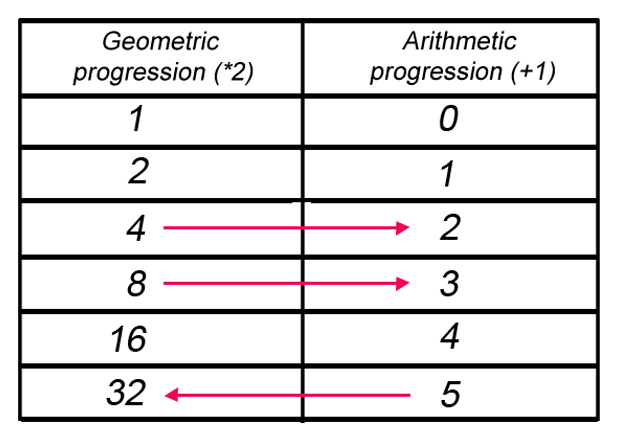
The first column is a geometric progression with base 2 and the second column is an arithmetic progression with a common difference of 1.
If we want to multiply 4 and 8, we would add the corresponding terms in the second column. That would give us 2 + 3 = 5. When we check the term corresponding to 5, we can see that it is 32, which we know is the value of 8 * 4.
In this way, we simplified multiplication to addition. Similarly, we can do division with subtraction. However, the problem with this demonstration is that it doesn’t have all numbers. One look shows that 3, 5, 6, 7 and others are missing. The gap between numbers increases as we go up. To fix this, different geometric and arithmetic progressions need to be used.
When we use a geometric progression and arithmetic progression and combine them in a similar way to form a table, they surprisingly form the “natural” logarithm table. But at that time, it wasn’t recognized as logarithms with base e.
Natural logarithms, as we now know them, first came into the picture when mathematicians attempted to calculate the area under the square hyperbola.
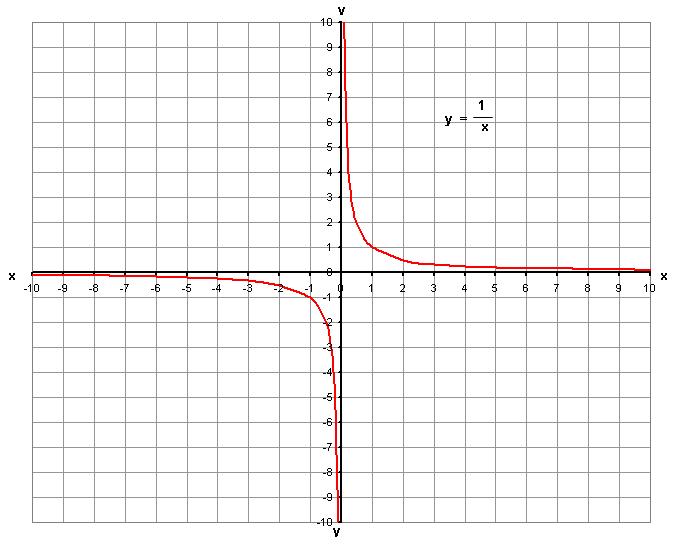
The equation of this curve is x y = 1.
If we integrate it, the answer will be ln(x). This was the first time logarithms were identified as functions, rather than just calculation tables. The name itself would come later, when Nicholas Mercator published the Taylor series for ln (1+x) and called logarithms with base e “natural logarithms”.
Also Read: What Is Euler’s Number?
Why Are Natural Logarithms “Natural”?
If anyone searched the literature for a suitable answer to this question, they would come across a couple reasons.
Exponential Growth
A primary reason is the concept of exponential growth or natural growth.
Exponential growth is a particular model of growth in which growth is directly proportional to the quantity at that time. Mathematically,
dx/dt = x
dx/x = dt
This implies that:
t = ln (x) + C
or
x(t) = x0ekt
where x0 is the initial amount, and k is the growth rate.
This model is applicable to multiple cases in nature. We see it in the growth of bacteria or simple population models, compound interest, the decay of radioactive materials, and so on.
Let’s look at a physical example to understand this model.
Imagine a case where I invest $100 with a 100% growth rate and it gets compounded every year; after one year, I will have $200. However, if I invest the same amount with 50% interest, but compounded twice, I will have $225 by the end of one year. And, when the number of times the amount gets compounded increases sufficiently… eureka! It converges to the value of e.
The Simplest Derivatives
Another possible reason that natural logarithms get their name is that they have much simpler derivatives than logarithms with any other base. For the function y = ln(x), its derivative is dydx= 1/x. This makes it easy for the natural log to be more involved in calculus, and is therefore of more use in mathematical calculations.
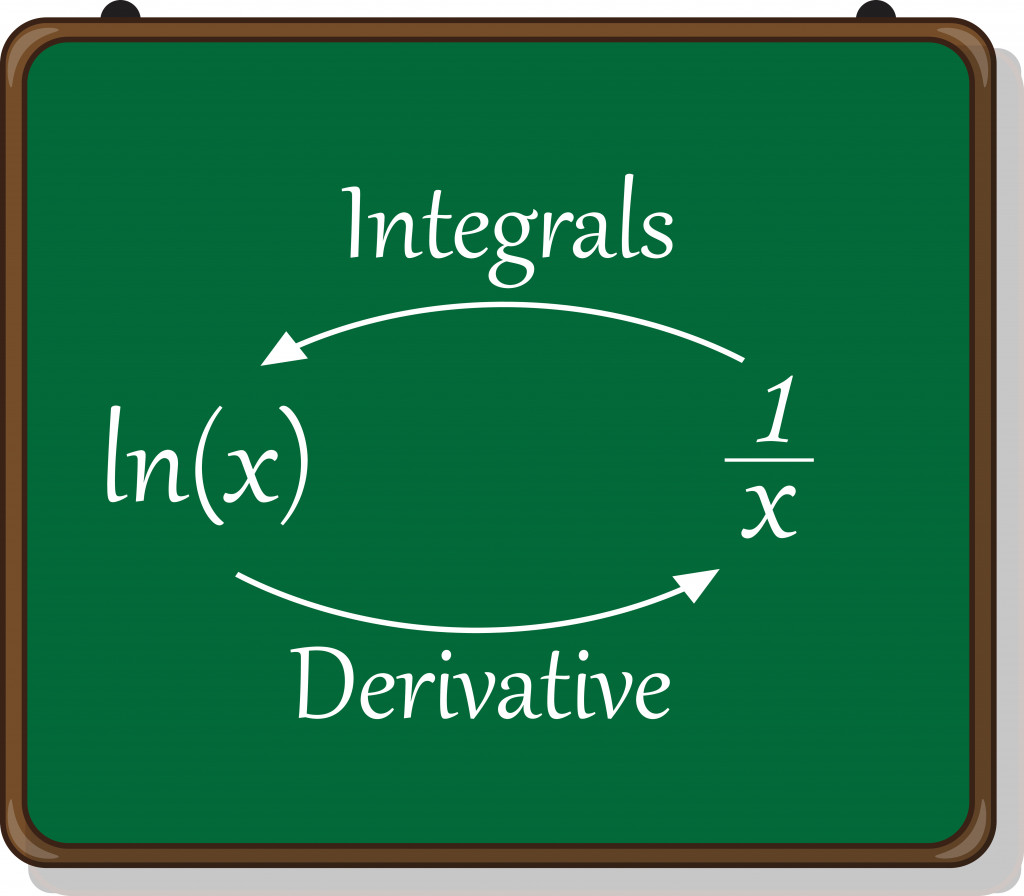
In order to find the derivatives of any other logarithms, we need to find the natural logarithm of that base.
When y = logb x, we get-
dy/dx = 1/ln (b) * 1/x
Thus, a natural logarithm becomes a base for the fundamental calculation of other log functions.
Conclusion
It is very evident that the natural logarithm got its name before it got its significance, before the value of e, other applications that we use today, and the many other possible applications that are yet to be discovered.
Yet, we can all agree on how unique natural logarithms are in comparison to other log functions, so it seems quite fair to refer to them as such!
How well do you understand the article above!

