How To Win Every Game Of Rock-Paper-Scissors?

To win every game of rock-paper-scissors, the player must use game theory to predict the opponent’s moves.

This is your third and final attempt – your last chance. All your hopes and dreams are at stake. On the other side of this much-awaited opportunity lies either rapture or suffering. Periodically, you move your hand up and down, as if demanding order in a court, a court filled with a tumult caused by your impatient self.

As your hand descends for the final time, the passage of time slows down. In the microsecond now scaled up to seconds, you see his two fingers gradually protrude, like the ears of an aloof dog. Surely, it must be scissors? You throw a rock. But wait, his adjacent fingers bloom as well… it’s paper!

The paper wraps the boulder entire. You lose. Your brother wins fair and square. Now hand him the remote.

The outcome of a toss can often determine the outcome of the match before it is even played. Furthermore, in competitive sports, the consequences of a loss can be even more dramatic than what happened to me. Yes, the results may be more repugnant than being unable to watch some SpongeBob.

One must be prepared, for we fight a battle every day. These battles take place during boring lectures, or on your local basketball court to decide who’ll pick first. They also might be the ugly – but necessary – battles with your own kin for the possession of authority over a powerful and irresistible weapon – the remote.

Humans Are Predictably Irrational

First, I want to address an important question. The illogicality of why paper beats rock is above me. However, that objection finds it very difficult to deter conformists or overturn the force of habit. Also, objectors abstain from raising this objection, for fear of being accused as a “nerd”, “buzzkill” or “spoilsport”, and attract public vilification.

Before going to war, we must first strategize, but to strategize, we must first gather some data. This requires mathematics and psychology. The data concerns the weight we give to the probabilities of every decision the game allows and the dispositions upon which the opponent might make them.

The discipline of mathematics that combines psychology and math to scrutinize decisions and decision makers in this way is known as Game Theory. Game Theory finds its applications in economics, politics and evolutionary biology too!

Now, I reckon that everyone is familiar with the rules: Paper beats rock, rock beats scissors and scissors beat paper. This dynamic can be represented by moving clockwise between the vertices of a triangle. In total, there are 9 decisions that spring from 3 strategies — three lead to a victory, three to a draw and three to defeat. Each strategy can then be played with an equal probability of one out of three.

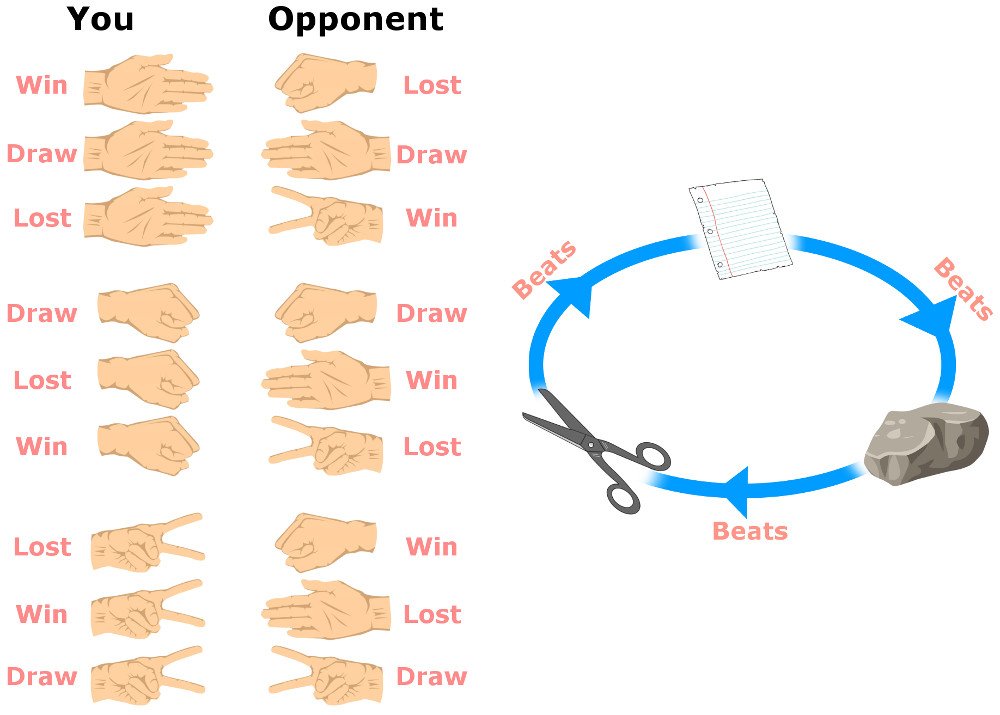
However, this knowledge of probabilities is only lucrative when the opponent deploys his strategies randomly, like a computer. This is how the game should be ideally played, but in reality, the human psyche comes into play. We do not make our decisions randomly. Humans introduce a component of irrationality; to predetermine outcomes then we require some data about how people tend to play. This peculiarity has rendered humans to be dubbed as predictably irrational.

Also Read: How Does Game Theory Deal With Irrational Actors?

The Game Plan

This is exactly what researchers at a Chinese university did. They conducted a study where 360 students were asked to incessantly play games of Rock-Paper-Scissors. Each game comprised 300 rounds, so the activity took at least two hours! Yes, people played Rock-Paper-Scissors for two hours straight!

The researchers gathered extensive data on how people played, which led them to two important findings. First, people who win tend to repeat their strategy; second, losers change. For instance, if I play rock and you play scissors, I’m highly likely to play rock again. And why not? It worked once, so why not give it another try? The latter’s reasoning also has a similar ground – it did not work, why would it work again?

Also Read: Can Economics (Game Theory) Help You Win A Game Of Chess?

How To Win Rock Paper Scissors

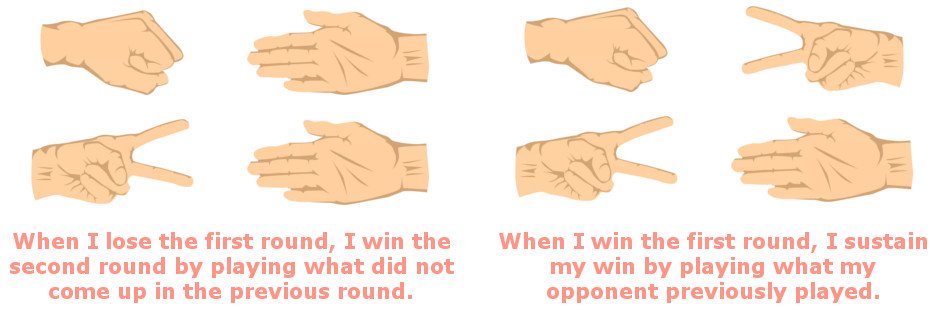
Keeping in mind “win-stay and lose-shift” we can devise two strategies to win.

1. If you lost the previous game, say, you played rock and your opponent played paper, he is highly likely to stay with his strategy and play paper again. Knowing this, you must play scissor, or to generalize – when you lose, play what did not previously come up.
2. If you won the previous game, say, you played rock and your opponent played scissor, your opponent is highly likely to change his strategy and play paper. Knowing this, and this is really confusing, you must play what will beat what he plays thinking that what he plays will beat what you previously played, as he is bound to change his approach. Or simply, play what he just played.

However, one question still dangles, what happens when we draw? This is tantamount to asking…

How Do We Start The Game?

This is particularly critical when a game might not be in the best-of-category. This implies that we must play randomly. However, can we be truly random? Is the game then driven by the whims of luck?

Not really. Like a tell in Poker, something could give us away. One could at least guess what his opponent might play by carefully studying his mannerisms, such as examining the position of his hand. People in tournaments (of course there are tournaments) often resort to shouting a move to distract and make their opponents uncertain. However comical, it has proven to be quite effective. Otherwise, starting randomly is what is advised.

Also, if the strategy delineated above is known to both players, they could second-guess or third-guess and keep guessing their opponent’s moves. The probabilities would stack up precariously and the math would become painstakingly complex. Professionals, like a chess grandmaster, might be good at this, but your brother… probably not.

However, when it comes to compounded probabilities, algorithms fare pretty well. Iocaine Powder was a program that won the first International RoShamBo Programming Competition in 1999. It devised 6 mega strategies based on past performances to defeat second- and so on guessing.

It is because of our predictably irrational nature that Rock-Paper-Scissors is not preferred for tosses. They are not truly fair or random, but to be completely honest, neither are coin tosses!

How well do you understand the article above!

Can you answer a few questions based on the article you just read?

Start Quiz

Question

Your answer:

Correct answer:

Next

You got {{SCORE_CORRECT}} out of {{SCORE_TOTAL}}

SHARE YOUR RESULTS

ShareTweetPinEmail

Your Answers

Retake Quiz