Table of Contents (click to expand)
Eratosthene calculated the circumference of Earth by measuring the length of a stick’s shadow in Alexandria and the distance between Alexandria and Syrene on foot. He then took the inverse tangent of the ratio between the shadow’s length and the stick’s length to find the angle of inclination of the Sun. He calculated the total circumference of the Earth to be ((360/7.2) x D ) kilometers, with D being the distance between Alexandria and Syrene.
This might come as a surprise for our younger readers, but throughout history, not everything that people learnt could be found on the Internet. Before that, humans “wasted” time poring over books, and before books, our ancestors had to communicate knowledge verbally! With that in mind, how is it possible that someone could accurately predict the circumference of the Earth without ever using a computer?

The Problem
Ancient astronomy was a puzzling field, with men using only visual observations, rather than the help of complex instruments. Even if they did have the intellectual prowess to tackle certain problems, most early scientists had to battle social and religious conventions. The idea of a spherical Earth appeared in Greek philosophy from Pythagoras in the 6th century BC and was sneered at because until then, Earth was considered completely flat! Aristotle provided evidence for the spherical shape of the Earth on empirical grounds by 330 BC, which is very slow progress when you think about it.

The problem with determining the Earth’s circumference held no importance if the Earth was flat, but gradually, once people started to acknowledge the actual shape, they needed to know exactly how big our world truly was. The only tool that astronomers had in 300 BC was their ability to recognize patterns.
Also Read: How Did People Figure Out That The Earth Was Round Without Any Technology?
The Man For The Job
Eratosthene was a Greek mathematician and the chief librarian at the Library of Alexandria. He is also credited for inventing the discipline of geography. His method for determining the size of the Earth was an elegant application of simple geometry to an otherwise very difficult problem. Although he took some small liberties with facts and made a number of assumptions, his calculations were pretty accurate. What’s even more amazing is the fact that this epic calculation took him a negligible amount of time, given that all his calculations could be done by hand using simple trigonometry.

Also Read: How Do We Know The Mass Of The Earth?
The Method
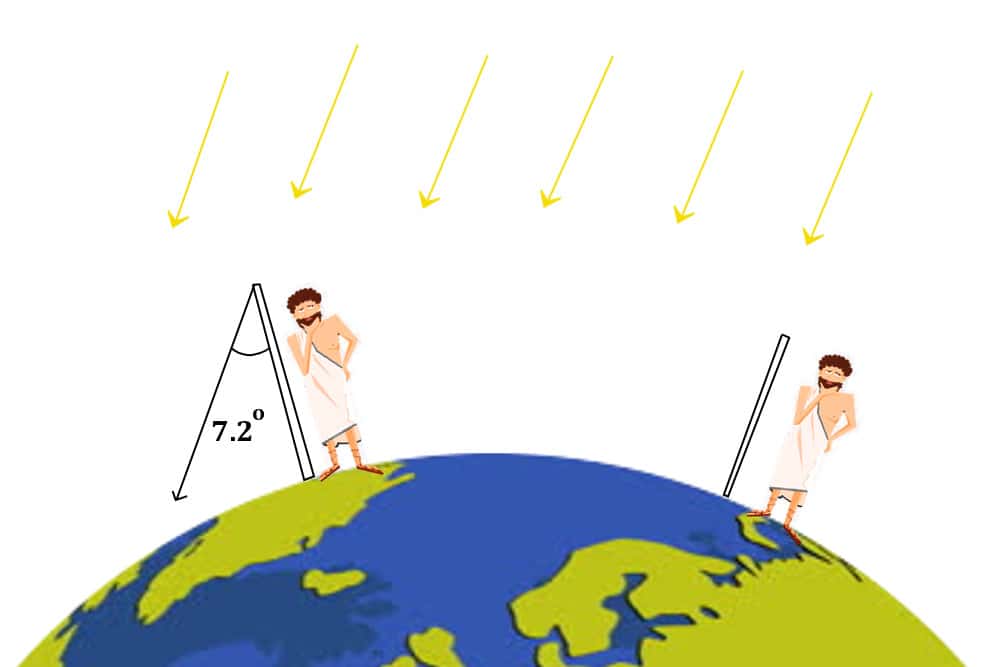
Eratosthenes knew that the Sun was directly overhead in the town of Syrene, in southern Egypt, on the Summer Solstice. Since the Sun was directly overhead, a well situated in that town didn’t cast a shadow at its bottom. He also knew that his hometown of Alexandria was further north of Syrene, and the exact distance on foot between the two cities was easily determined.
Next, he measured the length of a tall stick called a ‘gnomon’ and stuck it in the ground in Alexandria. When the sun’s rays struck the gnomon, it cast a shadow. Because the sun was directly overhead in Syrene, it had to be obliquely tilted if observed from Alexandria. Hence, a shadow of the stick could be observed in the latter town.
The length of the shadow and the actual length of the stick allowed Eratosthenes to calculate the angle of inclination of the Sun. This can be done by taking the inverse tangent of the ratio between the shadow’s length and the stick’s length.
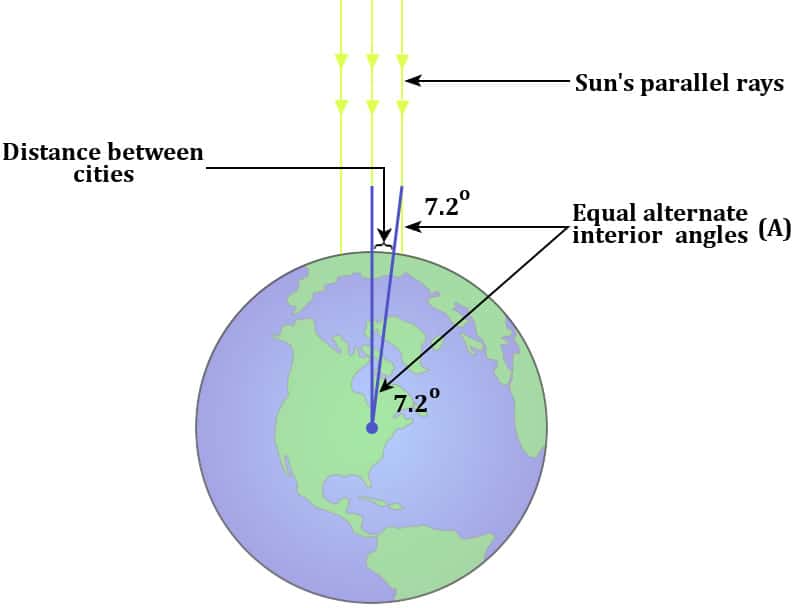
The angle labelled “A” is shown in the illustration above. By simple rules of geometry, it can also be observed that A is the angle subtended from the center of the Earth by the distance between the two cities. This angle was found to be nearly 7.2 degrees.
Now that Eratosthenes knew the subtended angle and the actual distance between the two cities of Syrene and Alexandria, he could calculate the total circumference of the Earth. The concept he used was very simple.
Distance between Alexandria and Syrene = D kilometers
Angle subtended by them on the center of the Earth= 7.2 degrees
Total angle of a circle= 360 degrees
Total Circumference of the Earth= ((360/7.2) x D ) kilometers
The unit of measurement that was popular in Greece at the time was stadia. Historians have yet to figure out the true length of a single stadia, but popular estimates put it around 160 meters. Eratosthenes estimated the circumference to be 252,000 stades, which is approximately 40,074 kilometers.
Shockingly enough… the real polar circumference is only 66 kilometers greater than this estimate!

The Estimation
The few assumptions that Eratosthenes made were trivial, but they need to be mentioned anyway. He assumed that the Sun was sufficiently far away from the Earth, so that its rays were always falling in parallel at the two cities. However, in reality, the rays at Syrene and Alexandria are ever so slightly inclined. Another liberty that he took was assuming that the distance between Syrene and Alexandria was very small, as compared to the circumference of the Earth, so it could be treated as a flat surface, rather than the arc of a larger circle. Needless to say, the Earth isn’t a perfect sphere and the two cities do not lie on the same latitude. Although the calculation is slightly flawed, this primitive technique provided an answer with only a 0.16% error, which is rather phenomenal!
The Advantages
Firstly, it was of paramount importance for us to find out how big our home actually was! Geographical research improved by leaps and bound following this determination. Through the study of eclipses, the size of the moon and the Sun was also easier to estimate, since we knew how big of a shadow the Earth cast, relative to its size. We even had a better understanding of seasons and their predictability.

Christopher Columbus studied what Eratosthenes had written about the size of the earth, but instead chose to believe another geographer named Toscanelli, who calculated the Earth’s circumference and came up with a result roughly 33% smaller than the actual value. Had Columbus set sail believing that Eratosthenes’ larger circumference value was more accurate, he would have known that the place he made landfall was not Asia, but rather the real New World, now known as America!

How well do you understand the article above!

