Ant-Man has never shrunk to a size small enough to create a black hole. Even if he did, there’s no way to predict what would happen.
All of us, at some point in our lives, have faced the question: “What superpower would you choose if given a choice?” Ranging from Superman to Captain America, you have some excellent options to choose from.
In this vast list, Ant-Man’s powers are among those that are based heavily on human scientific research.

Even though he has possessed quite a few powers throughout the wide array of comics in which he has featured, Ant-Man’s primary power is still true to his name: He can shrink to the size of an Ant. In fact, he can shrink to a size much smaller than an Ant, even being capable of going subatomic!
How Does Ant-Man Shrink?
According to the media, Ant-Man shrinks due to a particle known as the Pym particle. This fictional particle is a rare group of subatomic particles that can alter the space between atoms. When Scott Lang shrinks, his body gets packed into a much smaller form. All the muscle that you’d find in the body of a 5’10” tall man weighing 80kg is crammed into a body the size of an Ant—or even smaller.
According to Marvel, his body’s mass remains the same. His volume, however, vastly decreases. Since density=mass/volume, his body’s density increases exponentially. Subsequently, when he’s smaller, his strength and agility are significantly increased. This is why he can jump higher, punch harder, and perform at superhuman levels despite being so tiny
However, how does this work when he goes subatomic? Wouldn’t he risk turning into a black hole and destroying human life as we know it?
To analyze this possibility, we’re going to delve into the concepts of physics where this idea comes from: How black holes are formed and what a Schwarzchild radius is.
Also Read: What Would Happen If Ant-Man Were Real?
The Formation Of Black Holes
A black hole is formed when the center of a massive star collapses in on itself, forcing all of the star’s contents into a comparatively minuscule area. This collapse causes the star to release massive energy blasts into space, turning the star into a supernova. As this energy dies out, the star turns into a black hole.

To turn into a black hole, the star must be large enough and contain enough mass to become one. Black holes are formed specifically due to this mass getting packaged into a body with a significantly smaller radius. This radius is known as the body’s Schwarzchild radius.
Also Read: How Many Black Holes Are There In The Universe? How Do We Estimate This Number?
Schwarzchild Radius
Theoretically, the Schwarzchild radius (also known as the gravitational radius) of a body of mass M is the radius into which the body must be shrunk to undergo an irreversible gravitational collapse. This radius, represented by RG, is calculated using the formula: RG=2GM/c2, where G is the universal gravitational constant, and c is the speed of light.
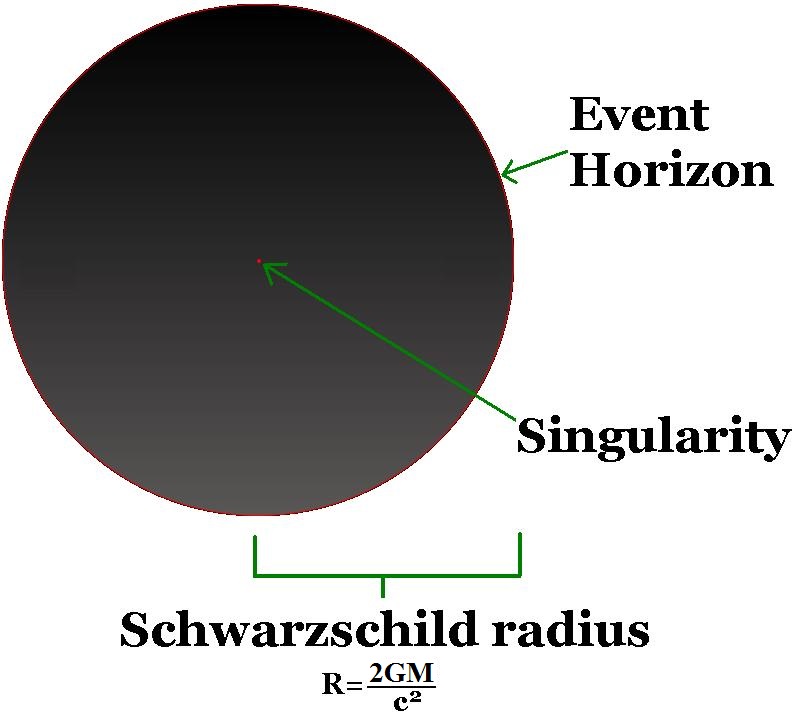
The Sun is a relatively small star, so its Schwarzchild radius is about 3 kilometers. Therefore, for the Sun to turn into a black hole, it would have to shrink into a ball with a radius equaling 3 kilometers or less.
Ant-Man’s Schwarzchild Radius
For a human being, this radius would be around 10-23 centimeters. If you remember what the radius of an atom is, you already know the answer to this article. The radius of an atom is about 10-8cm. Furthermore, the radius of an atom’s nucleus is about 10-13cm.
Now, Ant-Man, at his smallest, reaches a size where atoms are comparable to his size. This is what Marvel refers to as the quantum realm. So, at his tiniest, he can shrink down to 10-14cm, which is far greater than a human body’s Schwarzchild radius. This also explains why there is not a massive blast of energy when he shrinks.
However, owing to Scott Lang’s nature and the fact that he can’t control exactly how much his size changes, if he could shrink below 10-23 cm, there’s a high probability that he’d have done it already. What could that have led to?
Also Read: What’s The Biggest Scientific Mistake In Ant-Man?
What If Ant-Man Does Shrink Below His Schwarzchild Radius?
The concept of the Schwarzchild radius is based on Einstein’s field equations. The Schwarzchild metric is an exact solution to these equations, but they’re still just an assumption based on our limited data on black holes.
The assumption is that since heavenly bodies act as they do when subjected to such drastic changes in mass, that’s how a human body would work as well. There is simply no way to determine whether this assumption holds true.
Furthermore, the Schwarzchild metric is considered accurate because it is a solution to Einstein’s field equations. However, an interesting fact about these equations is that, according to our research, they’re wrong.

These equations require the energy and momentum of all quantum particles to be defined at the time of calculation. However, according to research considered accurate today, obtaining the precise position and momentum of a quantum particle is impossible. This is known as Heisenberg’s uncertainty principle.
What all of this means is that even if Ant-Man were to surpass his body’s Schwarzchild radius, there would be no way to know whether he’d turn into a black hole or not.
Is It Possible For Ant-Man To Turn Into A Black Hole?
Human beings simply do not possess enough information about black holes or energy to accurately determine the nature of these incredible phenomena. All we have is assumptions, and according to these assumptions, Ant-Man hasn’t turned into a black hole yet because he has never shrunk to a size small enough to cause the gravitational collapse a black hole requires.

Even if he was capable of crossing that threshold, we would have no way to predict what would happen. For a layperson like you and me, that basically means that we hope there’s no actual Ant-Man out there who could shrink to a size that small, just to be on the safe side.
How well do you understand the article above!

References (click to expand)
- Measuring Density. Goddard Institute for Space Studies
- J Wall. What Is a Black Hole?. Tration
- Black Holes. Georgia State University
- The Schwarzschild Metric. University of California, San Diego
- 18.1 Final thoughts on the Einstein field equation. web.mit.edu
- What Is the Uncertainty Principle and Why Is It Important?. California Institute of Technology
