Table of Contents (click to expand)
A double pendulum is simply two pendulums connected end to end. This system demonstrates chaos theory and how small variations lead to large changes.
A double pendulum is a system so simple that a fifth-grader could make it. Even so, this system and its motions are complex and extremely intriguing.
How a double pendulum moves around is a demonstration of chaos—a fundamental idea with far-reaching implications.
What Is A Double Pendulum?
A simple pendulum is a mass suspended from a fixed point. We see it inside pendulum clocks, relentlessly going back and forth to tell us the time. It gives us oscillatory motion, which is simple to trace. You give it a push, and it oscillates to and fro until frictional forces conspire to make it come to rest at the equilibrium position.

A double pendulum is exactly what it sounds like. It’s a simple system consisting of a pendulum with another pendulum attached to its end. Double the fun.
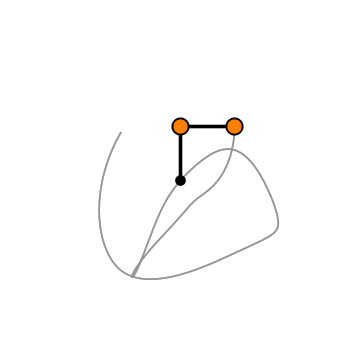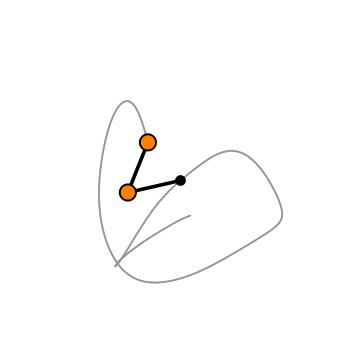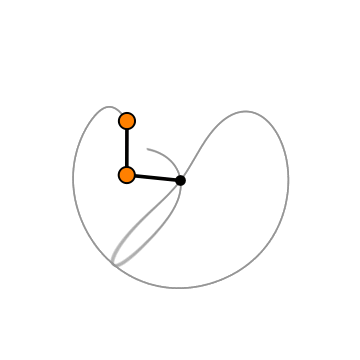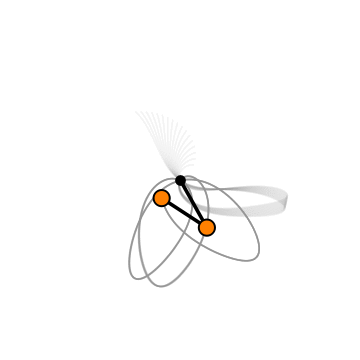
The motion of a double pendulum isn’t quite as simple as that of our single pendulum.
Also Read: How Does A Pendulum Clock Work?
Simple Pendulum Vs Double Pendulum
A simple pendulum will undergo oscillatory motion and come to rest at the equilibrium position. That is as certain as the sun rises in the east, so to speak. It’s entirely predictable.
If you plot the motion of the pendulum, its angle from the vertical on the x-axis, and its velocity in on the y-axis, you would get an inwardly tightening spiral. You could vary the initial conditions and make the spiral smaller or bigger, but ultimately the spiral ends at the same position. This graph is called a phase space.
Consider an ideal version of a simple pendulum—a point mass suspended by a massless rod. Friction and air resistance are not in the picture. If you plot it, you will get a loop. It doesn’t matter what the amplitude of the pendulum is, it will just be a different-sized loop.
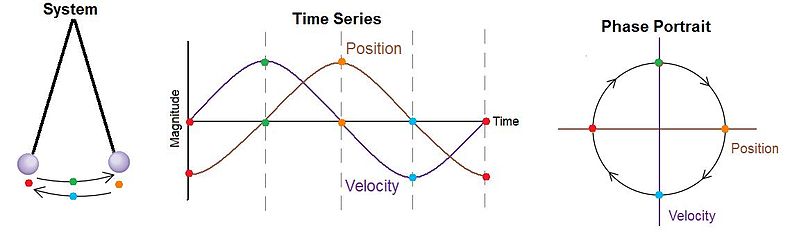
It doesn’t matter how you vary the initial conditions. If you have friction, it will always come to rest in the origin of the spiral. If you don’t, it will keep tracing a closed loop.
This means that the motion of a simple pendulum is predictable, which is exactly what a double pendulum is not.
Why the double pendulum and not the simple pendulum? A simple pendulum has only one degree of freedom. The double pendulum has two degrees of freedom. We need differential equations dependent on initial conditions to solve the motions of a double pendulum. This gives us the ingredients for chaos.
The Motion Of A Double Pendulum
The path of motion of a double pendulum looks crazy… because it kind of is! For small angles, double pendulums also give us simple harmonic motion, but for larger displacements, this is not the case. You can try out a live simulation of a live pendulum here.

We can describe the motion of a double pendulum using a system of ordinary differential equations. We must go to Lagrangian mechanics to figure out the equations of motion for double pendulums. If you want to know how these equations are derived, check out the video below.
This may seem confusing to some readers. If we have the equations of motion, why would the system be unpredictable? Solve the equations and we can predict the motion of the pendulums, right?
The trouble is that the system of the double pendulum is extremely dependent on initial conditions. If we cannot determine the initial conditions with 100% certainty (and in physics, we don’t throw around percentages lightly), we cannot predict the behavior of the system.
Since it is impossible to achieve that level of certainty, we cannot predict the motion of a double pendulum. Two double pendulums released from the same spot simultaneously will have a slight variation in their initial conditions. This will translate into a dramatic change in trajectory in a very short time. The variation in their paths will increase rapidly and exponentially.

The complexity of a double pendulum as opposed to a single pendulum is somewhat like the infamous three-body problem. You can predict the behavior of two bodies that influence each other, but add one more, and the system becomes too complex.
The Double Pendulum And Chaos Theory
A double pendulum is one of the simplest demonstrations of chaos theory. You may know this as “the butterfly effect”, but there is much more to it. One of the defining characteristics of chaos is sensitivity towards variation in initial conditions.
In the video below, the creator has made a simulation of 500 double pendulums with slight differences in their starting angles. By slight, I mean one-millionth of a radian. Two adjacent double pendulums are initially only different by one-millionth of a radian. They start out tracing the same paths. But as you can see, within seconds, their paths diverge dramatically.
This happens because of the chaotic nature of the system.
The point to note here is that this system is chaotic, but not random. It’s just very, very sensitive to initial conditions. If you have two double pendulums with the exact same initial conditions, they would trace the same path. The system is simply very unforgiving towards even a teeny tiny change. It will most certainly make a mountain out of a molehill.
However, in reality, it is impossible to release two double pendulums with the exact same initial conditions. Therefore, it will be impossible to predict the path the pendulum will trace.
This is a peek into how all chaotic systems work. The double pendulum demonstrates how we cannot make accurate predictions about chaotic systems.
When numerous instances are taken together, chaotic systems like double pendula do form patterns, called fractals.
Also Read: What Is Chaos Theory?
The Unpredictability Of The World
We see how chaotic behavior makes a system as simple as two balls on two strings nearly impossible to predict. What patterns would a million double pendulums released together make? What about triple pendulums?
Our world comprises a number of such impossible-to-predict and chaotic systems. Even our solar system exhibits chaotic behavior when you consider longer periods of time. Through the double pendulum example, we see chaos theory in action and can understand how difficult it is to predict the world around us!
How well do you understand the article above!

References (click to expand)
- Shinbrot, T., Grebogi, C., Wisdom, J., & Yorke, J. A. (1992, June). Chaos in a double pendulum. American Journal of Physics. American Association of Physics Teachers (AAPT).
- Double Pendulum -- from Eric Weisstein's World of Physics. Wolfram Research, Inc.
- The Simple Pendulum - Graduate Program in Acoustics. The Pennsylvania State University
