Table of Contents (click to expand)
The reuleaux triangle is made when circles are drawn from the vertices of equilateral traingles. Its constant width and curved edges make it appropriate for many applications.
Aside from a circle, what other shapes can a manhole be so that it won’t fall through the hole? One of the answers to this question is a Reuleaux triangle.

A Reuleaux triangle, also called a spherical triangle, is a shape made with intersecting curves when circles are drawn from the vertices of an equilateral triangle. This shape has a constant width when rotated, which makes it useful for many purposes. Studied by the legendary likes of Leonardo da Vinci and Leonhard Euler, it is used in various applications, such as mechanical motors, architectural windows, guitar picks and graphical signages, among others.
Construction Of Reuleaux Triangle
The Reuleaux Triangle is named after Franz Reuleaux, the 19th-century German engineer who advanced the study of machines by converting one form of energy into another. He used this specialized triangle in many of his designs.
The construction of the Reuleaux Triangle is fairly straightforward:
- Make an equilateral triangle
- Using a compass, draw a circle, taking one of the vertexes as the midpoint and connecting the other two vertices on the edge of the circle being drawn.
- Repeat step 2 by taking the other points as the center, respectively.

Also Read: Euler’s Identity: ‘The Most Beautiful Theorem In Mathematics’
Mathematical Properties Of Reuleaux Triangle
Curve With A Constant Width
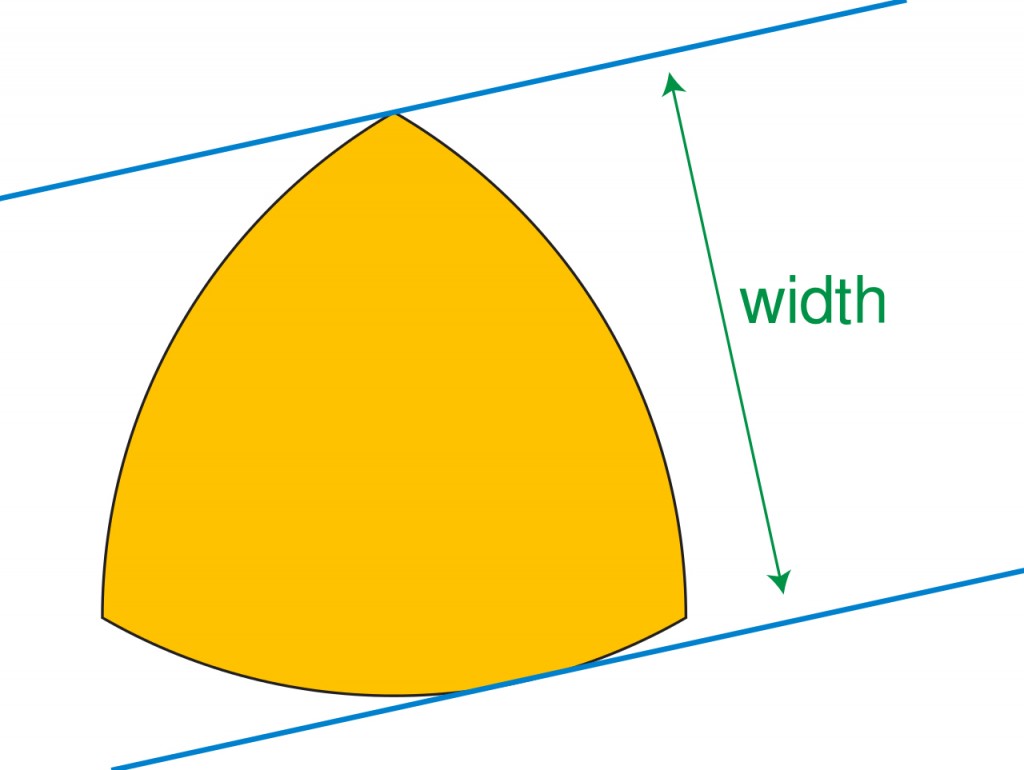
The first clear property that the Reuleaux Triangle shows is its constant width when two parallel supporting lines are drawn from any surface, regardless of the orientation of the lines. The distance between the parallel lines is the radius of the circle drawn from the vertices to make the Reuleaux Triangle.
A Rotating Motor
The Reuleaux Triangle shows the sharpest angle between the vertex of any shape that has a curve of constant width. Each pair of the arc makes an angle of 120°.
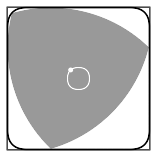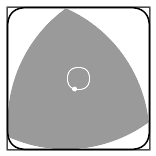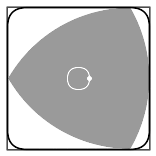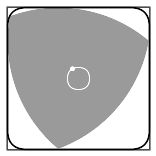
The Reuleaux Triangle can be used as a rotor within a square; it can perform a complete rotation and stay inside the square while doing so, touching every surface of the inside of the square. It is a rotor with the minimum possible area. It follows a curve made by pieces of four different ellipses, as its axis doesn’t stay at a single point while rotating. The 120° angle of the triangle doesn’t let the rotor touch the extreme edges of the square, making a curved-edge square. The rotating Reuleaux Triangle traces out 98.77% of the area of the square.
Also Read: What Is Ptolemy’s Theorem?
Applications Of Reuleaux Triangle
Due to its compact geometry and equal proportions, the Reuleaux Triangle is used as a fundamental basis of structural and rotational strength. Some of the applications are:
Pencils
Modern pencil design has seen the adaptation of the Reuleaux Triangle as its predominant form. The triangle enables a stronger grip. As a person writes with three fingers, each curve of the triangle supports a finger, which provides better overall control of the pencil.

Guitar Picks
Similar to the pencil, guitar picks use the base geometry of the Reuleaux Triangle for better control and a tighter grip. It is easier to manipulate the strings with one of the edges of the curve while holding two fingers to hold the other two. Variations of the Reuleaux Triangle pick are even used for different genres of music to generate different sounds.

Carving Squares
As noted earlier, the Reuleaux Triangle is one of the best ways to create a square with small curved edges. The constant curve width and irregular rotating motion help in carving out a clean square.
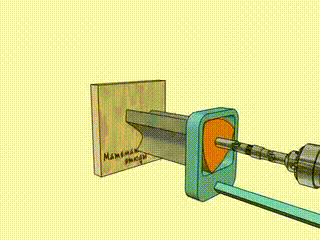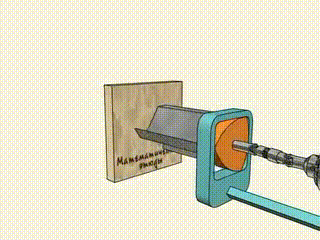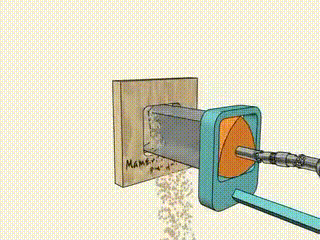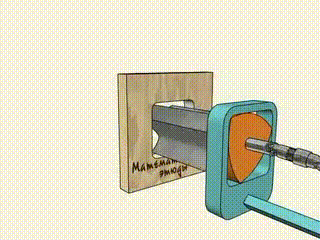
Mechanism Design
Franz Reuleaux intensively studied the mechanical properties of a Reuleaux Triangle. The triangle can be used as a mechanical linkage that converts rotation around an axis into motion. This rotating property can be seen in the Wankle engines used in cars and bikes.

Some early film projectors have also used the triangle to project images. The Luch-28mm film projector uses it as a key piece in the rotation of the mechanism.
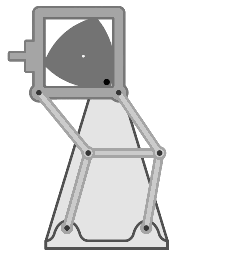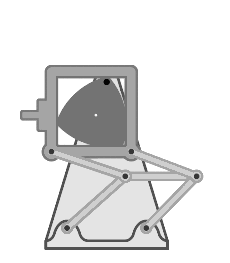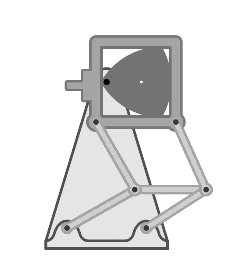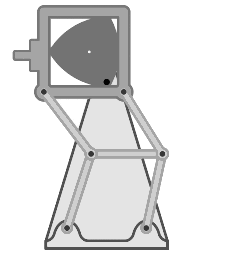
Architecture
The Reuleaux Triangle has been extensively used in architectural forms. Its compact geometry and sturdy structural integrity make it highly versatile and aesthetically pleasing to the eye. In the late 13th or early 14th century, it was used as a decorative feature in many churches, mainly as a window design of the facade.

This shape is also used in staircase design. The 2D form of a triangle is used as the base plan for the staircase. The stairwell is then arranged on the three curves while the remaining center area is kept as a cavity.

In modern architecture, this triangle has been applied in high-rise buildings with the geometrical shape as its cross-section. A building in Cologne, Germany called the Kölntriangle has a total gross floor area of 84,300 m2 (907,000 sq ft). The curves of the triangle provide panoramic views on three sides of the building, while also providing varying depths to the rooms arranged along the curve.

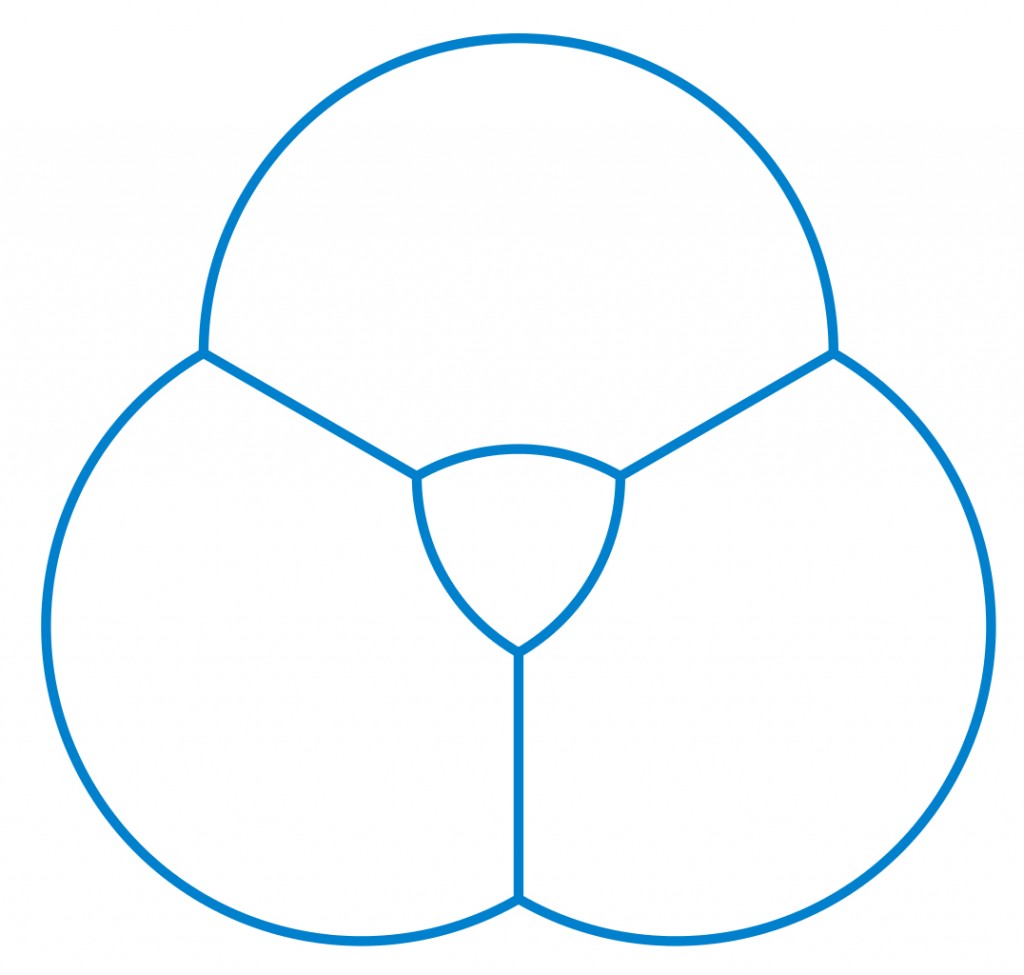
In Nature
The structure of soap bubbles has intrigued scientists for centuries, as it forms a fractal-like arrangement of varying sizes of bubbles.

Plateau’s law states that the 2D soap bubbles meet at 120°, the same angle as a Reuleaux triangle. Based on this law, it is possible to construct Reuleaux Triangles inside the intersecting bubbles.
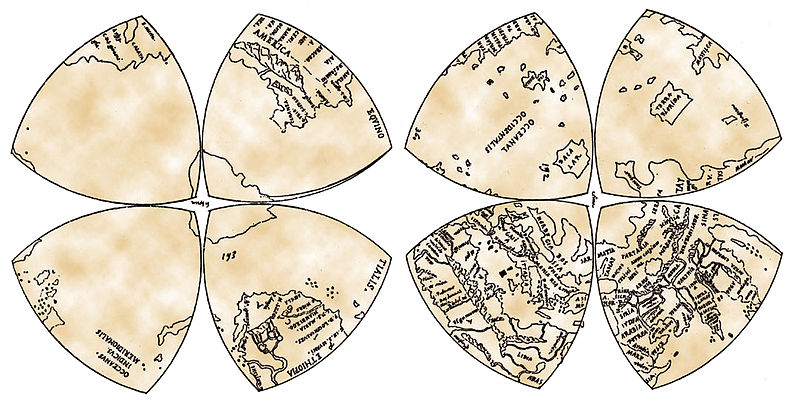
Map Making
Leonardo da Vinci made maps of the world based on the geometry of the Reuleaux Triangle. He took 8 of these shapes and divided them into two parts to make the surfaces of the earth. Each Reuleaux Triangle represents 1/8th of the world. It is called Leonardo da Vinci’s Mappamundi.
In Closing
The Reuleaux Triangle has been used in many ways and in many things. Its three equal curved side and constant curve width make it desirable for many applications. Its structural stability and the small perimeter have seen its application in architecture and mechanical design as well. To this day, many new approaches to its application are being explored on new products.
How well do you understand the article above!

