Which Has A Higher Gravitational Pull, A Stationary Or A Rotating Object? Why?

A stationary object has a greater gravitational pull than a rotating object of the same dimensions.

Over the centuries, various theories have been formulated to explain physical phenomena. One such phenomena is the attraction of objects towards the Earth. Many scientists and philosophers in the ancient world tried to explain this observation. In the 17^th century, Newton formulated the first explicit mathematical model for gravity in his book, Principles of Natural Philosophy, which was groundbreaking and launched a new epoch in natural sciences.

Newtonian gravity ruled the discussion until the 20^th century, when Einstein formulated his General Theory of Relativity.

General Relativity gives the most accurate picture of gravity to date, but is mathematically quite rigorous. Moreover, for most applications, Newtonian gravity works just fine without going very deep into challenging mathematics. Therefore, the answer to the question posed in the title of this article will be obtained using Newton’s theory. Apologies in advance to those who love relativity… you can check this out for a deeper dive on general relativity.

Fundamentals Of Newtonian Gravity

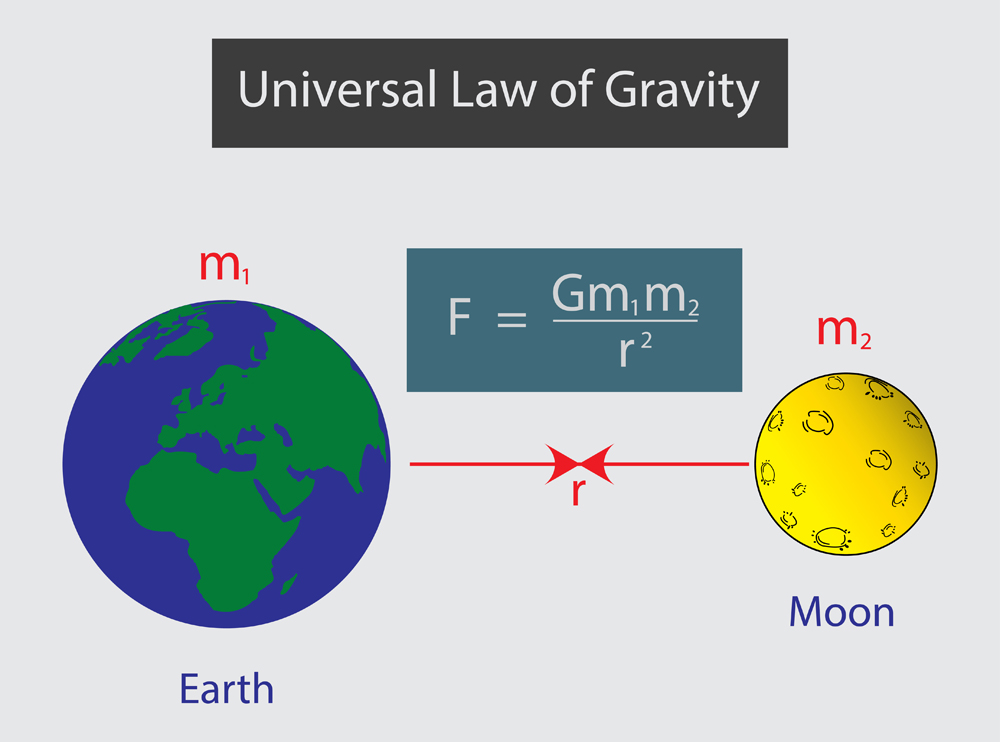
Newtonian theory is based on observations of nature (empiricism). Gravity is a force that attracts two masses separated by some distance and always acts along the line joining the center of mass of both the objects. To be more precise, the attractive force between two objects is proportional to the product of the two masses and the reciprocal of distance squared. Mathematically, gravitational force, F:

where,

G = Universal Gravitational Constant ~ m³/kg/s²

= mass of object A

= mass of object B

r = distance between the two masses

Also Read: Why Do All Objects Fall Towards The Ground At The Same Rate, Regardless Of Their Weight?

Mechanics Of Rotating Objects

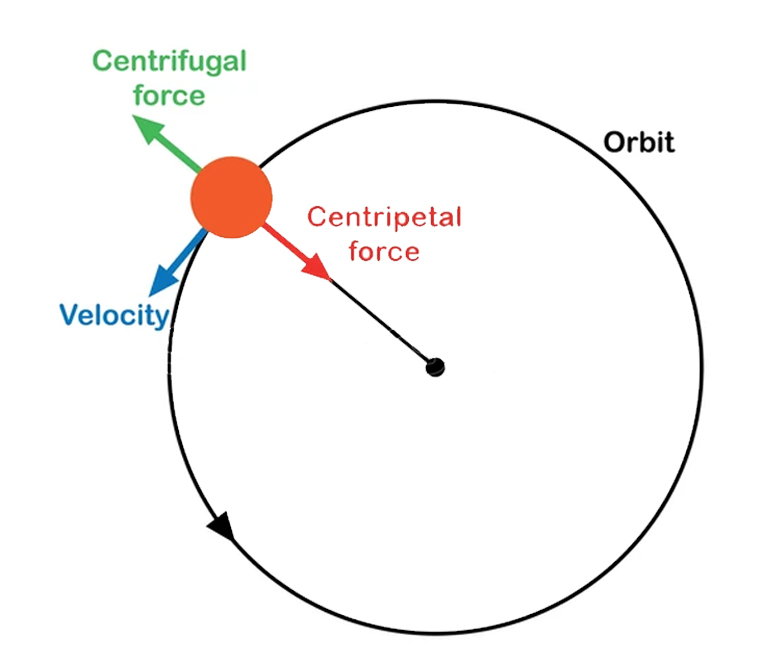
A mass rotating in a circular path experiences the following forces:

• An inertial force that acts along a tangential direction (at 90^o to the radius). If the mass were to be released from orbit, then it would move along the tangential path.
• A force directed towards the center of the circular path, along the radial line, is called centripetal force. This force is responsible for keeping the mass in orbit.
• A force directed away from the center of the circular path, along the radial line, is called centrifugal force. This is a fictitious force that pushes mass away from the center of orbit and is a reaction to centripetal force.

Mathematically, centripetal force, F_cp :

where,

m = mass of the object rotating in a circular trajectory

v = linear velocity of rotation

r = radius of circular path

= (v/r) = angular velocity (amount of rotation within a fixed time interval)

F_cp is a real force experienced by the object. According to Newton’s 3^rd  law, when a force acts on a body, the body exerts an equal reaction force in the opposite direction. Thus, the fictitious centrifugal force, F_cf arises, which is equal in magnitude, but opposite in direction to F_cp .

Therefore,

Here, the negative sign (-) signifies the opposite direction to F_cp .

Also Read: What Are Centripetal Acceleration And Centrifugal Force?

Dynamics Of A Two-Body System

In physics, whenever two or more forces act on a particle simultaneously, the resultant force is the vector sum of the individual forces. A vector sum is a mathematical operation similar (but not identical) to simple algebraic addition, but also takes into account the direction of the forces.

For easier calculations, let’s assume the presence of a perfect sphere, having mass M and radius R. The sphere can be modeled as a collection of infinitesimally thin (extremely thin) circular disks placed on top of each other. The radius of the central disk (equatorial line) is maximum, i.e., R, and the radius of the poles is zero.

Consider the following cases:

CASE 1: The sphere does not rotate

The gravitational force experienced by a small object of mass m, at a distance r from M is:

Here, M>>>m and r<<<R (this approximation is analogous to satellites orbiting the Earth).

Since the sphere is not rotating, centrifugal force, F_g is zero. Net force on m:

CASE 2: The sphere starts rotating

Now, assume that the sphere of mass M and radius R starts rotating, with its axis of rotation along the +z direction. Gravitational force is:

Centripetal and centrifugal forces start acting on the surface of the sphere. F_cf is maximum at the equator (-Mw²R) and minimum at the poles (approaching zero). The magnitude of centrifugal force, F_cf at the equator and poles is given by:

Therefore, the net force on m due to gravitational attraction from M and the rotation of M about the +z axis is:

The Answer

The development of centrifugal force due to the rotation of an object results in a decrease in the net force experienced by m at the equatorial plane. The net force increases away from the equator, and reaches its maximum at the poles, exactly equal to the gravitational force. This decrease in gravitational pull, however, is negligible for slow rotation, like that of the Earth. In fact, the acceleration due to gravity, g, is 9.764 m/s²  at the equator and 9.863 m/s² at the poles.

Thus, a stationary object has a greater gravitational pull than a rotating object of the same dimensions.

How well do you understand the article above!

Can you answer a few questions based on the article you just read?

Start Quiz

Question

Your answer:

Correct answer:

Next

You got {{SCORE_CORRECT}} out of {{SCORE_TOTAL}}

SHARE YOUR RESULTS

ShareTweetPinEmail

Your Answers

Retake Quiz