Why Is A Full Circle 360 Degrees, Instead Of Something More Convenient, Like 100?

A full circle is 360 degrees because the Babylonians used the sexagesimal system. It also represents the number of days a year and also because 360 is highly composite.

The other day, I helped my 12-year-old cousin with his math homework. His homework had questions about the area of a circle with a certain radius and circumference. The questions seemed quite simple, and we were able to solve them all in 15 minutes.

What annoyed my cousin all the time, however, was, why was a complete circle 360 degrees? Why not something simpler like 10 degrees or 100 degrees? All calculations would have been so easy; wouldn’t that be more convenient?

Hypothesis 1: Mathematical Reasons

You may wonder what mathematical reasons there might be for using 360 degrees to represent a complete circle since 360 always seems to cause difficulties in calculating the answers to your math homework.

But actually, it is the ideal solution. A number like 10 or 100 would have been mathematically more uncomfortable.

The number 360 is divisible by any number from 1 to 10, except the 7th. It is actually divided into 24 different numbers: 1,2,3,4,5,6,8,9,10,12,15,18,20,24,30,36,40,45,60,72,90,120,180 and 360 itself. These 24 numbers are called the divisors of the number 360.

This is the highest number of divisors for each positive integer up to its own value of 360. In contrast, the number we often wish would be the value for the full circle—100—has only 9 divisors.

This property of the number 360 makes it a strongly composite number. Numbers are said to be highly composite if they are positive integers with more divisors than any smaller positive integer has. Highly composite numbers are considered good base numbers with which to perform common calculations.

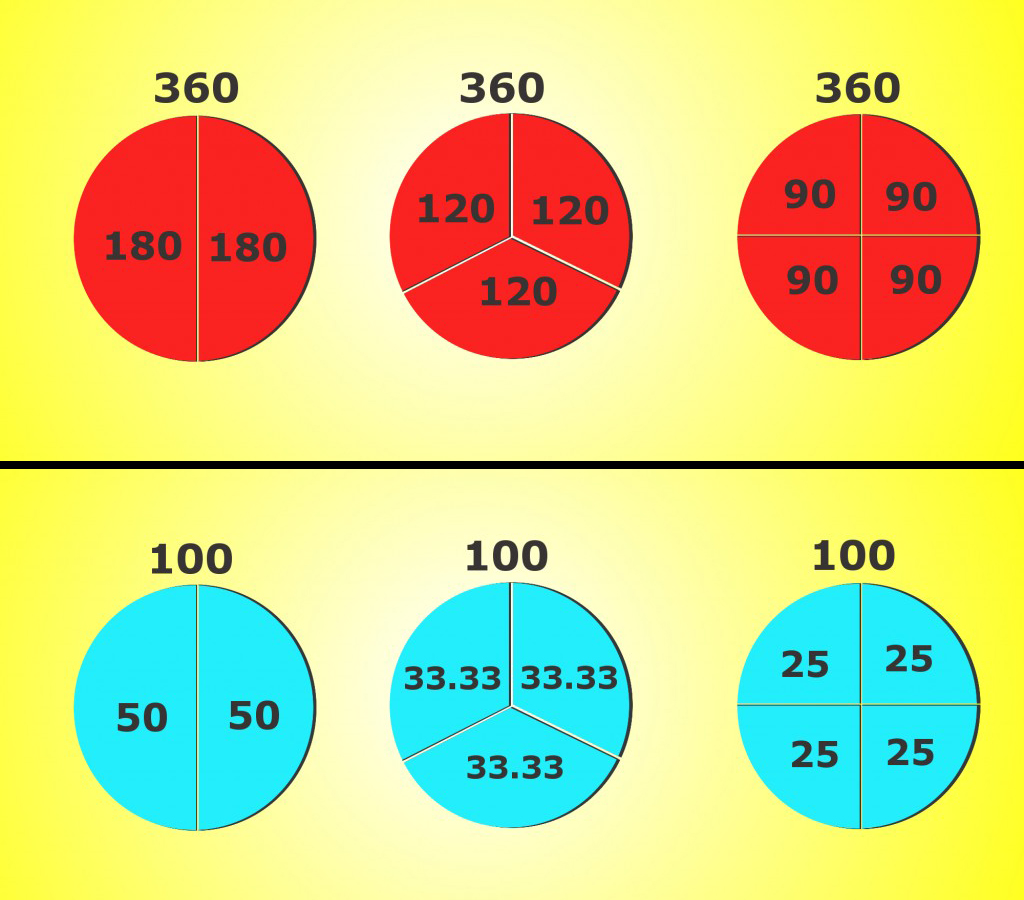
For example, 360 can be divided into two, three and four parts and the resulting number is a whole number. The resulting numbers are 180, 120 and 90.

However, dividing 100 by three doesn’t end in a whole number. Instead, it provides a decimal value of 33.3 recurring, which makes performing calculations difficult. Calculations using 360 actually become pretty simple once you’re smart enough to do them in your head and can put down the calculator.

But is this the whole justification? Was this the only reason why our ancestors decided to break a circle in 360 degrees?

Also Read: Do We Have Any Mathematical Proof That Pi Is Infinite?

Hypothesis 2: The Length Of A Year

Have you ever wondered why there are exactly 365 days a year? Why not use a more convenient number like 300 or 400?

Okay, there is no mathematical reason for this, but it is just an observation made by our ancestors, and these observations also contributed to a circle being closed by 360 degrees.

The ancient astronomers, especially the Persians and Cappadocians, noticed that it took the sun 365 days to return to exactly the same position.

In other words, the sun advances one degree every day on its elliptical orbit. Persians had a leap month every 6 years to compensate for the 5 extra days. Moreover, the lunar calendar has a total of 355 days, while the solar calendar has 365 days. And, which number sits perfectly between the two and is a composite number?

Yes… 360!

Hypothesis 3: Historical Reasons

Another theory that suggests why a full circle is 360 degrees comes from the Babylonians. The Sumerians and Babylonians famously used the Sexagesimal number system.

The sexagesimal system is one with a base value of 60, while the current system we use is known as the decimal system and has a base value of 10. So once we reach the 10th number, we start repeating the symbols of earlier numbers from 0 to 9 to form new numbers.

The Babylonians had 60 different symbols to make numbers with. Why should they use 60 again?

Because 60, like 360, is a highly composite number with up to 12 factors. Just as we can count 10 on our fingers for the decimal system, we can also count up to 60.

Start by counting the knuckles of the 4 fingers (not the thumb) on your right hand. 12, right?

Now, on the other hand, raise any of those fingers to remember that you finished one iteration and got the number 12. Now, repeat the same procedure as many times as the number of fingers remaining on the left hand.

The number you will end up with is 12 knuckles x 5 fingers = 60.

But Anyway… Why 360?

If we were to draw an equilateral triangle with the length of sides equal to the radii of the circle and place one of its vertexes at the center of the circle, then we could fit a total of 6 such equilateral triangles inside a circle. Since the Babylonians used the sexagesimal numeral system, they considered each triangle to have a base value of 60. Thus, 6 triangles x 60 base value again gives us a value of 360.

The Indian Context

There is even evidence that a circle in the Rigveda from India was divided into 360 parts.

Twelve spokes, one wheel, navels three.
Who can comprehend this?
On it are placed together
three hundred and sixty like pegs.
They shake not in the least.
— Dirghatamas, Rigveda 1.164.48

Next time someone asks you this question, I hope you have something to say!

Also Read: Why Are There 24 Hours In A Day And 60 Minutes In An Hour?

Wanna check how much information you retained from the article?

Can you answer three questions based on the article you just read?

Start Quiz

Question

Your answer:

Correct answer:

Next

You got {{SCORE_CORRECT}} out of {{SCORE_TOTAL}}

SHARE YOUR RESULTS

ShareTweetPinEmail

Your Answers

Retake Quiz