Table of Contents (click to expand)
A projectile’s motion is parabolic because it is affected by gravity. Gravity causes the projectile to fall in a curved path, rather than a straight line. The equation for projectile motion takes into account the force of gravity, which is why the path of a projectile is always a parabola.
Why does a cannonball shot from a cannon not descend vertically, but rather curvilinearly? Why does a tossed javelin draw a sumptuous arc before it stings the ground? Regardless of the nature of the projectile, the arc one draws through the air is precisely a parabola.
The reason is, of course, gravity, the only force that affects its motion (neglecting air resistance) after it is projected. However, what we are essentially asking is, why does gravity force it to trace a parabola? Kepler knew that the planets orbited the Sun in an ellipse, but he didn’t know why they did so. In that same vein, Why doesn’t a projectile trace any other shape but a parabola?
The Equation
Of course, this is not true when a projectile is projected perpendicular to the Earth’s surface. To observe a parabolic trajectory, we must project it at some angle with the surface. Even though no horizontal forces affect a projectile following its launch, it is the initial horizontal force that makes the glorious journey possible. How else could a javelin travel a horizontal distance if it were not provided with a horizontal force?
In the 17th century, mankind had yet to build a rocket and the most powerful telescopes couldn’t look further than Saturn. Despite these constraints, how could Newton, sequestered in a tiny room in England, discover that the planets orbit the Sun and not – as the most eminent philosophers of the time believed (or rather hoped) – in a circle, but rather an ellipse? Mathematics, of course.
Newton proved Kepler’s claim by discovering a relationship between the distance between Earth and the sun, and the angle it spans while rotating around it. He discovered that it was exactly the same relationship that describes a point tracing an ellipse. However, his evaluation was based on his newly proposed law of gravity. If his law were untrue, his proof would also fall apart. We now know that what he proposed was true; Newton never explained what gravity is, but he beautifully explained how it works.
Similarly, to determine which curve a projectile traces, we must find an equation that describes its motion and the curve that corresponds to it.
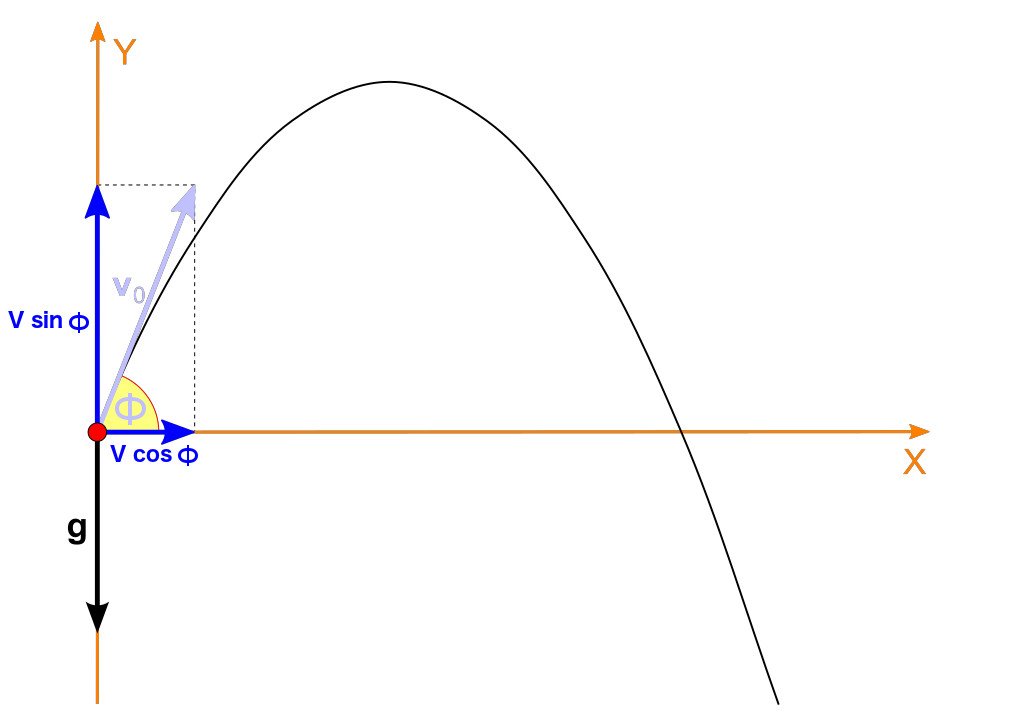
The projectile is projected with an initial velocity ‘v’ at an angle ‘Φ’ with respect to the surface. The distance the projectile travels horizontally (on the X-axis) is given as x = vtcosΦ (v=x/t). However, the distance it travels vertically (on the Y-axis) is given as y = vtsinΦ – (½)gt². This is because vertically, the projectile experiences a force and thus acceleration, namely, the acceleration due to gravity, denoted by ‘g’.
Also Read: Defying Gravity: Must What Go Up, Always Come Down?
Now, because this acceleration is constant, we can use the kinematic equation s = ut + (½)at² to calculate the distance ‘y’. Here, ‘u’ is the initial velocity, which in this case is vsinΦ and ‘a’ is the constant acceleration, which in this case is ‘-g’, due to our selected convention. Therefore, the vertical distance y = vtsinΦ – (½)gt².
To find ‘y’ in terms of ‘x’, or to obtain an equation that describes the relationship between ‘y’ and ‘x’, we solve for ‘t’ in the first equation and substitute its value in ‘y’.

or, 
Substitute the value of t in: 


Also Read: What Is Orbital Velocity?
Here, tanΦ and g/2v²cos²Φ are constants, so the equation uncannily resembles the equation y = ax+bx² – the equation of a parabola!
How well do you understand the article above!

